线段树

线段树定义

线段树是一种特殊的平衡二叉查找树，使用线段树，可以实现数据的添加、查找和删除等操作。相比二叉查找树，线段树不同的地方在于，线段树的根节点表示了一个完整的单元区间，线段树中的内部节点，将整个区间划分成了更小的子区间，而叶节点代表了区间间隔为1的单位区间。

基本概念

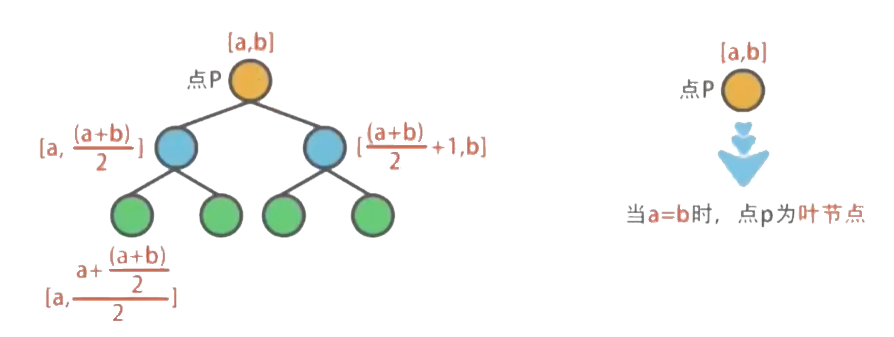
对于线段树中的任意一个节点P, 如果它表示区间 :
它的左孩子区间为 , 右孩子区间为
当左右节点相等，即 时，该节点为叶子节点

线段树的存储

可以用数组来存储线段树
令树的根节点为 ,对于任意节点 ,它的父节点下标是 ,左孩子下标是 ,右孩子下标是

C++实现

class SegmentTree
{
    using ll = long long;
    ll n, m;
    vector<ll> t, a, tag; // t为线段树，a为原始数组，tag为懒标记

    // 上推操作
    void push_up(ll fa)
    {
        t[fa] = t[fa << 1] + t[fa << 1 | 1];
    }

    // 下推操作
    void push_down(ll l, ll r, ll fa)
    {
        ll mid = (l + r) >> 1;
        t[fa << 1] += tag[fa] * (mid - l + 1);
        tag[fa << 1] += tag[fa];
        t[fa << 1 | 1] += tag[fa] * (r - mid);
        tag[fa << 1 | 1] += tag[fa];
        tag[fa] = 0;
    }

    // 建树
    void build(ll fa, ll l, ll r)
    {
        if(l == r) {
            t[fa] = a[l];
            return;
        }
        ll mid = (l + r) >> 1;
        build(fa << 1, l, mid);
        build(fa << 1 | 1, mid + 1, r);
        push_up(fa);
    }

    public:
    // 构造函数
    // n: 原始数组长度
    // a: 原始数组
    SegmentTree(int n, vector<ll> &a)
    {
        this->n = n;
        this->a = a;
        this->t.resize(a.size() * 4);
        this->tag.resize(a.size() * 4);
        build(1, 1, n);
    }

    // 区间和查询
    // [ql, qr]区间内的和
    ll query(ll ql, ll qr, ll l, ll r, ll fa)
    {
        if(ql <= l && qr >= r)
            return t[fa];
        ll ans = 0, mid = (l + r) >> 1;
        push_down(l, r, fa);
        if(ql <= mid)
            ans += query(ql, qr, l, mid, fa << 1);
        if(qr > mid)
            ans += query(ql, qr, mid + 1, r, fa << 1 | 1);
        return ans;
    }

    // 区间更新
    // [ql, qr]区间内的每个数加上k
    // fa为当前节点的父节点
    void update(ll ql, ll qr, ll l ,ll r, ll fa, ll k)
    {
        if(ql <= l && qr >= r) {
            t[fa] += k * (r - l + 1);
            tag[fa] += k;
            return;
        }
        push_down(l, r, fa);
        ll mid = (l + r) >> 1;
        if(ql <= mid)
            update(ql, qr, l, mid, fa << 1, k);
        if(qr > mid)
            update(ql, qr, mid + 1, r, fa << 1 | 1, k);
        push_up(fa);
    }
};

此代码通过给定的数组构造线段树，可以实现查询区间和以及给某个区间的每个数加上一个数 的操作。
数组下标从 开始，查询和更新操作均为闭区间操作。
修改代码也可以实现其他操作，如区间最小值、区间最大值等。

构造参数:

1. n(int): 原始数组长度
2. a(vector): 原始数组

时间复杂度

• 构造:
• 更新:
• 查询: